Un bon mapa sempre ajuda!
Els mapes ens ajuden a entendre i preveure el món que ens envolta. Sense ells no podríem avançar de manera eficient. Les matemàtiques són l’eina que fan servir els científics per fer “mapes” de la realitat.
Un bon mapa ens ajuda a anar d’un punt a un altre de la manera més ràpida possible. Així, es podria dir que un mapa serveix per a solucionar un problema: “Com puc anar des d’on sóc fins on vull anar?”. Però els mapes fan molt més que això. D’un cop d’ull podem veure quina forma té el territori que estem estudiant. Per on passen carreteres i per on no hi passen. Podem copsar els punts més destacats i la distància aproximada que hi ha entre ells (quins estan a prop, quins són lluny…). No només ens ajuden a resoldre un problema sinó que també ens ajuden a entendre millor allò que ens envolta.
Un mapa és una representació esquemàtica de la realitat i, com a tal, deixa alguns detalls fora. Per exemple, no hi ha cap mapa que marqui la posició de cada arbre i cada fanal tot i que alguns d’ells sí que marquen fonts, que són uns objectes molt més petits. Per què? Doncs perquè qui va fer el mapa va considerar que no calia saber on era cada arbre però, en canvi, sí que és molt útil conèixer on pots apaivagar la teva set. Qui fa el mapa tria què és important i què no.
Finalment, els mapes ens suggereixen alternatives i noves rutes. Mirant un mapa de manera distreta podem descobrir nous punts d’interès o una ruta alternativa que potser no és tan curta, però resulta molt més pintoresca.
Models matemàtics, els mapes de la realitat
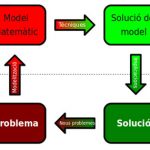
Quan un científic o un enginyer vol entendre millor allò que està estudiant fa servir un model matemàtic, que és l’equivalent abstracte dels mapes dels quals hem parlat. De fet, alguns d’aquests models matemàtics s’assemblen molt a un mapa de veritat i fins i tot es poden dibuixar. D’altres, però, són molt més complexos i cal l’ajuda d’ordinadors per estudiar-los i extreure’n la informació que estem buscant.
Un d’aquests models que s’assembla molt a un mapa de carreteres i podem dibuixar en un full de paper és el model que ens ajuda a resoldre un joc d’enginy que es coneix com les Torres de Hanoi. A Recerca en Acció hem preparat un joc interactiu que us ajudarà a entendre i fer servir aquest “mapa” per resoldre el joc.
Torres de Hanoi, Triangles de Sierpinski i Camins Hamiltonians
A l’interactiu podeu veure i manipular simultàniament el joc d’enginy i el seu model matemàtic. A la dreta de la imatge hem dibuixat el “mapa” que ens permetrà saber cap a on ens hem de moure. Cada posició legal del joc està representada per un punt i cada moviment legal està representat per una ratlla que uneix la posició de sortida i la posició d’arribada. Com podeu veure hem tingut molta sort i no només hi ha pocs punts i poques ratlles sinó que, a més, els hem pogut dibuixar de manera clara i simètrica.
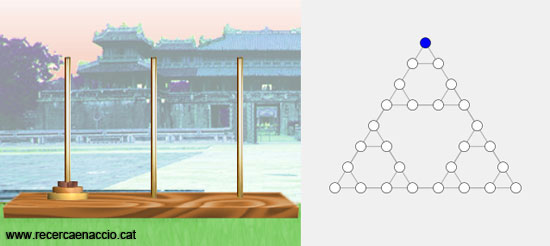
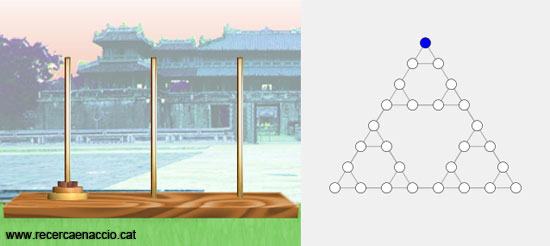
Posició inicial de les Torres de Hanoi de nivell 3.
Si ens fixem en el mapa veurem que té forma de triangle. Doncs bé, cadascun dels vèrtexs d’aquest triangle representa una posició final: tots els discs a l’esquerra, tots els discs al centre o tots els discs a la dreta. Sabent això resoldre el joc és molt fàcil. Només cal anar en línia recta seguint la vora del triangle!
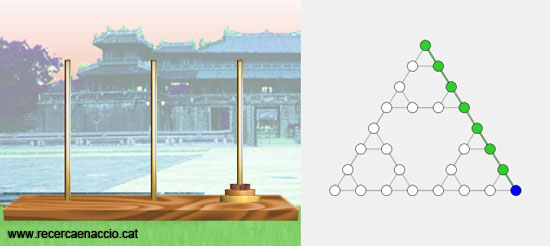
Posició final de les Torres de Hanoi de nivell 3.
Ara bé, aquest mapa està format per 3 còpies d’un mapa més petit i, a la vegada, cadascuna d’aquestes còpies està formada per 3 còpies d’un mapa encara més petit… Aquest esquema “fractal” que ens recorda al Triangle de Sierpinski ens està dient que segurament hi ha una solució recursiva al problema:
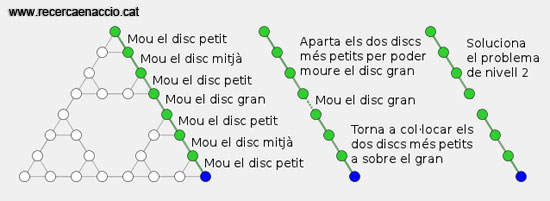
Descomposició de la solució òptima.
Com podeu veure per resoldre el joc de nivell 3 cal resoldre primer el joc de nivell 2 (per apartar els discos petit i mitjà), moure el disc gran a la seva posició definitiva i llavors tornar a resoldre el joc de nivell 2 per posar els discos petit i mitjà de nou a sobre del gran. De la mateixa manera per resoldre un joc de nivell N+1 cal resoldre 2 jocs de nivell N. Aquest patró l’hem après gràcies al fet que hem pogut observar el “mapa” d’aquest joc.
Finalment, i com ja hem dit abans, un “mapa” pot suggerir nous reptes, noves rutes. Per exemple, creieu que el joc de les Torres de Hanoi té un camí Hamiltonià (és a dir, un camí que passa per tots els punts sense repetir-ne cap)? I un cicle Hamiltonià (és a dir, un camí Hamiltonià que comença i acaba al mateix punt)?
Un mapa és una representació esquemàtica de la realitat i, com a tal, deixa alguns detalls fora. Per exemple, no hi ha cap mapa que marqui la posició de cada arbre i cada fanal tot i que alguns d’ells sí que marquen fonts, que són uns objectes molt més petits. Per què? Doncs perquè qui va fer el mapa va considerar que no calia saber on era cada arbre però, en canvi, sí que és molt útil conèixer on pots apaivagar la teva set. Qui fa el mapa tria què és important i què no.
Finalment, els mapes ens suggereixen alternatives i noves rutes. Mirant un mapa de manera distreta podem descobrir nous punts d’interès o una ruta alternativa que potser no és tan curta, però resulta molt més pintoresca.
Models matemàtics, els mapes de la realitat
Quan un científic o un enginyer vol entendre millor allò que està estudiant fa servir un model matemàtic, que és l’equivalent abstracte dels mapes dels quals hem parlat. De fet, alguns d’aquests models matemàtics s’assemblen molt a un mapa de veritat i fins i tot es poden dibuixar. D’altres, però, són molt més complexos i cal l’ajuda d’ordinadors per estudiar-los i extreure’n la informació que estem buscant.
Un d’aquests models que s’assembla molt a un mapa de carreteres i podem dibuixar en un full de paper és el model que ens ajuda a resoldre un joc d’enginy que es coneix com les Torres de Hanoi. A Recerca en Acció hem preparat un joc interactiu que us ajudarà a entendre i fer servir aquest “mapa” per resoldre el joc.
Torres de Hanoi, Triangles de Sierpinski i Camins Hamiltonians
A l’interactiu podeu veure i manipular simultàniament el joc d’enginy i el seu model matemàtic. A la dreta de la imatge hem dibuixat el “mapa” que ens permetrà saber cap a on ens hem de moure. Cada posició legal del joc està representada per un punt i cada moviment legal està representat per una ratlla que uneix la posició de sortida i la posició d’arribada. Com podeu veure hem tingut molta sort i no només hi ha pocs punts i poques ratlles sinó que, a més, els hem pogut dibuixar de manera clara i simètrica.

Posició inicial de les Torres de Hanoi de nivell 3.
Si ens fixem en el mapa veurem que té forma de triangle. Doncs bé, cadascun dels vèrtexs d’aquest triangle representa una posició final: tots els discs a l’esquerra, tots els discs al centre o tots els discs a la dreta. Sabent això resoldre el joc és molt fàcil. Només cal anar en línia recta seguint la vora del triangle!

Posició final de les Torres de Hanoi de nivell 3.
Ara bé, aquest mapa està format per 3 còpies d’un mapa més petit i, a la vegada, cadascuna d’aquestes còpies està formada per 3 còpies d’un mapa encara més petit… Aquest esquema “fractal” que ens recorda al Triangle de Sierpinski ens està dient que segurament hi ha una solució recursiva al problema:

Descomposició de la solució òptima.
Com podeu veure per resoldre el joc de nivell 3 cal resoldre primer el joc de nivell 2 (per apartar els discos petit i mitjà), moure el disc gran a la seva posició definitiva i llavors tornar a resoldre el joc de nivell 2 per posar els discos petit i mitjà de nou a sobre del gran. De la mateixa manera per resoldre un joc de nivell N+1 cal resoldre 2 jocs de nivell N. Aquest patró l’hem après gràcies al fet que hem pogut observar el “mapa” d’aquest joc.
Finalment, i com ja hem dit abans, un “mapa” pot suggerir nous reptes, noves rutes. Per exemple, creieu que el joc de les Torres de Hanoi té un camí Hamiltonià (és a dir, un camí que passa per tots els punts sense repetir-ne cap)? I un cicle Hamiltonià (és a dir, un camí Hamiltonià que comença i acaba al mateix punt)?












Felicitats per entomar aquest repte de visualitzar les matemàtiques
De moment l’inici és molt prometedor