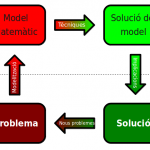
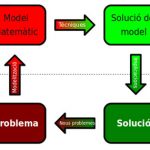
Els científics no poden ignorar les dades. Si les dades contradiuen el model cal revisar aquest últim i afegir (o treure!) allò que falta.
Hem explicat amb anterioritat com han de ser els models matemàtics i com els científics els creen tenint en compte factors com ara la seva simplicitat o la qualitat de les previsions que produeixen. Però el cert és que la feina d’un científic rarament parteix de zero. El més natural és “heretar” un model que s’hagi fet servir en estudis anteriors i millorar-lo amb nous coneixements i noves idees. Avui en veurem un bon exemple.
Hem parlat amb en Joaquim Fort, un científic del Departament de Física de la Universitat de Girona que fa servir els seus coneixements per entendre com es van estendre els canvis culturals que marquen la fi del Paleolític, on els humans eren caçadors-recol·lectors, i que inicien una nova era, el Neolític, on els humans van fer de l’agricultura el seu principal mitjà de vida.
Segur que us estareu preguntant què té a veure la física i la arqueologia… I segur que us quedareu encara més sorpresos quan us expliqui que l’anterior estudi de Joaquim Fort va tractar sobre el virus d’estomatitis vesicular, que produeix malalties al bestiar. I encara més, abans d’això havia estudiat en profunditat la física de les combustions.
Virus, flamarades i canvis culturals… Què tenen en comú tots aquests temes de recerca? Els qui seguiu aquest projecte des de l’inici segur que ja ho heu endevinat: comparteixen un mateix model matemàtic!
Un front d’ones per entendre’ls a tots!
En efecte, una infecció vírica, una deflagració o l’expansió d’un canvi sociocultural tenen el mateix comportament, a gran escala, que una ona que avança per un ramat, l’aire o un territori (respectivament).
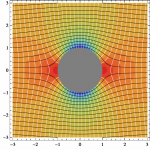
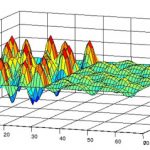
Així, per comprendre millor aquests fenòmens cal disposar d’un bon model matemàtic i Joaquim Fort porta molt de temps estudiant models que permeten simular i entendre la propagació del front d’una ona.
El front d’ona està format pel conjunts de punts que reben al mateix temps l’impacte d’una pertorbació. En els exemples anteriors parlaríem dels punts que comencen a cremar-se a la vegada, les cèl·lules que s’infecten en un mateix instant o els indrets on s’adopten uns determinats costums.
Fixeu-vos, per exemple, que la resolució temporal dels diferents fenòmens és ben diferent: mentre que una flamarada tarda pocs segons a produir-se, una infecció pot tardar dies i un canvi cultural segles sencers! L’espai que ocupa cada fenomen també varia significativament, mentre les infeccions tenen lloc d’ins d’uns quants milers de cèl·lules les flamarades ocupen ràpidament desenes de metres cúbics i les societats es mouen a través de continents sencers…
Malgrat tot, i aquesta és precisament la màgia de les matemàtiques, el comportament és el mateix si escollim l’escala adient per a cada fenomen. A més, la informació que ens interessa de cada fenomen és semblant: Quant tardarà una flama/infecció/canvi sociocultural en arribar a un punt donat? Quins punts rebran l’impacte d’aquests fenòmens a la mateixa vegada?

Fronts concèntrics formats per la caiguda d’una gota en un tanc d’aigua.
Les dades manen
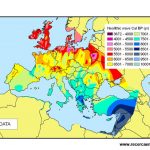
Però tenir un bon model per predir el comportament de les flamarades no sempre significa que puguem aplicar-ho a fenòmens com ara les infeccions o els moviments culturals. Quan Joaquim Fort va intentar predir el comportament del virus d’estomatitis vesicular es va trobar que les dades no es corresponien amb les prediccions fetes pels models clàssics de propagació del front d’ones. Pel cas de la transició del Paleolític al Neolític el model tampoc no funcionava. En tots dos casos la predicció indicava que la infecció i l’agricultura s’havien d’estendre molt més ràpidament del que els experiments i les troballes arqueològiques indicaven com ell mateix ens explica: “La velocitat implicada pels jaciments arqueològics és aproximadament un quilòmetre per any, però els models anteriors donaven una velocitat més ràpida que aquesta velocitat observada.”
Aquesta discrepància indicava que el model era incomplet i que calia afegir quelcom que el millorés. Fort ens ha promès explicar-nos aquesta millora en una propera trobada. Mentre arriba el moment, però, us demanarem que ens ajudeu… Quines diferències creieu que hi ha entre el comportament d’una flamarada i el d’una infecció? Per què les infeccions evolucionen molt més lentament? Creieu que amb els canvis socioculturals pot passar quelcom semblant?
MMACA, Museu de Matemàtiques de Catalunya
Hem parlat amb en Joaquim Fort, un científic del Departament de Física de la Universitat de Girona que fa servir els seus coneixements per entendre com es van estendre els canvis culturals que marquen la fi del Paleolític, on els humans eren caçadors-recol·lectors, i que inicien una nova era, el Neolític, on els humans van fer de l’agricultura el seu principal mitjà de vida.
Segur que us estareu preguntant què té a veure la física i la arqueologia… I segur que us quedareu encara més sorpresos quan us expliqui que l’anterior estudi de Joaquim Fort va tractar sobre el virus d’estomatitis vesicular, que produeix malalties al bestiar. I encara més, abans d’això havia estudiat en profunditat la física de les combustions.
Virus, flamarades i canvis culturals… Què tenen en comú tots aquests temes de recerca? Els qui seguiu aquest projecte des de l’inici segur que ja ho heu endevinat: comparteixen un mateix model matemàtic!
Un front d’ones per entendre’ls a tots!
En efecte, una infecció vírica, una deflagració o l’expansió d’un canvi sociocultural tenen el mateix comportament, a gran escala, que una ona que avança per un ramat, l’aire o un territori (respectivament).
Així, per comprendre millor aquests fenòmens cal disposar d’un bon model matemàtic i Joaquim Fort porta molt de temps estudiant models que permeten simular i entendre la propagació del front d’una ona.
El front d’ona està format pel conjunts de punts que reben al mateix temps l’impacte d’una pertorbació. En els exemples anteriors parlaríem dels punts que comencen a cremar-se a la vegada, les cèl·lules que s’infecten en un mateix instant o els indrets on s’adopten uns determinats costums.
Fixeu-vos, per exemple, que la resolució temporal dels diferents fenòmens és ben diferent: mentre que una flamarada tarda pocs segons a produir-se, una infecció pot tardar dies i un canvi cultural segles sencers! L’espai que ocupa cada fenomen també varia significativament, mentre les infeccions tenen lloc d’ins d’uns quants milers de cèl·lules les flamarades ocupen ràpidament desenes de metres cúbics i les societats es mouen a través de continents sencers…
Malgrat tot, i aquesta és precisament la màgia de les matemàtiques, el comportament és el mateix si escollim l’escala adient per a cada fenomen. A més, la informació que ens interessa de cada fenomen és semblant: Quant tardarà una flama/infecció/canvi sociocultural en arribar a un punt donat? Quins punts rebran l’impacte d’aquests fenòmens a la mateixa vegada?

Fronts concèntrics formats per la caiguda d’una gota en un tanc d’aigua.
Les dades manen
Però tenir un bon model per predir el comportament de les flamarades no sempre significa que puguem aplicar-ho a fenòmens com ara les infeccions o els moviments culturals. Quan Joaquim Fort va intentar predir el comportament del virus d’estomatitis vesicular es va trobar que les dades no es corresponien amb les prediccions fetes pels models clàssics de propagació del front d’ones. Pel cas de la transició del Paleolític al Neolític el model tampoc no funcionava. En tots dos casos la predicció indicava que la infecció i l’agricultura s’havien d’estendre molt més ràpidament del que els experiments i les troballes arqueològiques indicaven com ell mateix ens explica: “La velocitat implicada pels jaciments arqueològics és aproximadament un quilòmetre per any, però els models anteriors donaven una velocitat més ràpida que aquesta velocitat observada.”
Aquesta discrepància indicava que el model era incomplet i que calia afegir quelcom que el millorés. Fort ens ha promès explicar-nos aquesta millora en una propera trobada. Mentre arriba el moment, però, us demanarem que ens ajudeu… Quines diferències creieu que hi ha entre el comportament d’una flamarada i el d’una infecció? Per què les infeccions evolucionen molt més lentament? Creieu que amb els canvis socioculturals pot passar quelcom semblant?
MMACA, Museu de Matemàtiques de Catalunya















0 Comentaris