Tant se val si estem investigant física quàntica com si volem fer un truc de màgia, quan es tracta de models matemàtics com més senzill millor!
Heu jugat ja al joc interactiu del Laberint màgic? És un dels 4 jocs interactius que ha desenvolupat el Museu de Matemàtiques de Catalunya (MMACA) a Recerca en Acció amb el finançament de la Fecyt.
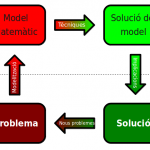
Quan un científic vol entendre un fenomen natural sovint recorre a la modelització matemàtica. La modelització matemàtica és, en aquest sentit, la primera eina que necessitem per tractar un problema. Així, quan resolem problemes a l’escola (d’aquells on un tren viatja cap a la dreta i un altre cap a l’esquerra i s’han de trobar, ja m’enteneu) el primer que fem és un senzill model que ens ajudi a entendre la situació i a aprofitar les eines matemàtiques de què disposem per a resoldre el nostre problema.
Ara bé, triar un model, no sempre és fàcil. Hi ha una infinitat de models en potència per a qualsevol problema donat i, com podreu suposar, no els podem provar tots! Així doncs, hi ha uns criteris generals que ajuden a triar el millor model per a cada situació. Un d’aquests criteris és que el model sigui prou acurat. És a dir, que la informació que obtinguem del model sigui prou acurada per ser útil (seguint amb l’exemple dels trens el nostre model ens hauria de dir a quina hora es troben amb una precisió de minuts o segons però no cal que encerti el nanosegon!).
Perquè un model sigui prou acurat el criteri fonamental per escollir entre diverses opcions és la simplicitat. Així, entre dos models que compleixin amb el criteri anterior escollirem sempre el que sigui més senzill. Hi ha molts motius per fer aquesta tria, motius filosòfics (com ara la famosa Navalla d’Occam) i motius pràctics (com ara que com més senzill sigui un model millor el podrem resoldre i més coses podrem aprendre del nostre problema. Sigui com sigui, a la pràctica resulta que hi ha models sorprenentment senzills i avui en veure’m un!
Màgia matemàtica
Dins del divers món de la màgia hi ha una branca coneguda com a màgia matemàtica que es dedica a produir trucs de màgia basats en fets matemàtics poc intuïtius. El joc del Laberint Màgic n’és un exemple.
El joc ens demana que ens movem lliurement per un laberint mentre algunes de les seves habitacions desapareixen. Afortunadament el mag (que en aquesta ocasió és virtual!) sempre fa desaparèixer habitacions on no hi som tot i que en cap moment li hem dit on érem!
Com ja hem dit, aquest joc de màgia pertany a la branca “matemàtica” i per tant es fonamenta en un fet poc intuïtiu. En aquest cas, el fet poc intuïtiu és que podem fer un model tan tan senzill del laberint que només necessitem pintar-lo de 2 colors!

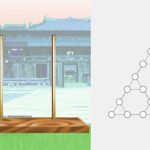
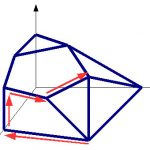
El laberint màgic pintat de 2 colors.
A la imatge podeu veure el Laberint Màgic amb les habitacions pintades de dos colors. Les que tenen una carta senar son més clares i les que tenen una carta parell son més fosques. Aquest senzill model és tot el que es necessita per fer el truc de màgia!
Quan el mag elimina una habitació i aquesta habitació no és la nostra el primer que ens diu la intuïció és que el mag sap on som i només elimina caselles desocupades. Però el mag no necessita tanta informació. En té prou a fer servir un model matemàtic molt més senzill que li digui, només, si som a una casella clara o fosca. Així, si som a una casella clara eliminarà només caselles fosques i si som en una casella fosca eliminarà només caselles clares. Tant se val a quina casella en concret siguem!
Però com pot saber l’ordinador a quina casella hi som, si no li diem? Molt senzill, fixeu-vos que cada carta fosca està connectada només a cartes clares i a l’inrevés, però mai no podreu trobar un passadís que connecti dues cartes fosques o dues cartes clares. Això significa que si ets a una casella clara i fas un nombre senar de passos acabaràs en una casella fosca i a l’inrevés. Per contra, si fas un nombre parell de passos romandràs al mateix color del que vas sortir. De nou, al mag no li cal saber cap on vas, només li cal saber d’on has sortir i quantes habitacions has visitat!
Ara bé, el nombre de passos que fas te’l diu ell mateix així que només li cal encertar a quina casella ets a l’inici de la partida. Algú podria pensar que l’ordinador és prou intel·ligent com per endevinar en quin any vas néixer però, de nou, la resposta és molt més senzilla. Ets capaç de trobar-la?
Digues-nos a partir de quin moment l’ordinador pot estar segur de si et trobes en una habitació parell (fosca) o senar (clara) i com ho ha fet.
MMACA, Museu de Matemàtiques de Catalunya
Quan un científic vol entendre un fenomen natural sovint recorre a la modelització matemàtica. La modelització matemàtica és, en aquest sentit, la primera eina que necessitem per tractar un problema. Així, quan resolem problemes a l’escola (d’aquells on un tren viatja cap a la dreta i un altre cap a l’esquerra i s’han de trobar, ja m’enteneu) el primer que fem és un senzill model que ens ajudi a entendre la situació i a aprofitar les eines matemàtiques de què disposem per a resoldre el nostre problema.
Ara bé, triar un model, no sempre és fàcil. Hi ha una infinitat de models en potència per a qualsevol problema donat i, com podreu suposar, no els podem provar tots! Així doncs, hi ha uns criteris generals que ajuden a triar el millor model per a cada situació. Un d’aquests criteris és que el model sigui prou acurat. És a dir, que la informació que obtinguem del model sigui prou acurada per ser útil (seguint amb l’exemple dels trens el nostre model ens hauria de dir a quina hora es troben amb una precisió de minuts o segons però no cal que encerti el nanosegon!).
Perquè un model sigui prou acurat el criteri fonamental per escollir entre diverses opcions és la simplicitat. Així, entre dos models que compleixin amb el criteri anterior escollirem sempre el que sigui més senzill. Hi ha molts motius per fer aquesta tria, motius filosòfics (com ara la famosa Navalla d’Occam) i motius pràctics (com ara que com més senzill sigui un model millor el podrem resoldre i més coses podrem aprendre del nostre problema. Sigui com sigui, a la pràctica resulta que hi ha models sorprenentment senzills i avui en veure’m un!
Màgia matemàtica
Dins del divers món de la màgia hi ha una branca coneguda com a màgia matemàtica que es dedica a produir trucs de màgia basats en fets matemàtics poc intuïtius. El joc del Laberint Màgic n’és un exemple.
El joc ens demana que ens movem lliurement per un laberint mentre algunes de les seves habitacions desapareixen. Afortunadament el mag (que en aquesta ocasió és virtual!) sempre fa desaparèixer habitacions on no hi som tot i que en cap moment li hem dit on érem!
Com ja hem dit, aquest joc de màgia pertany a la branca “matemàtica” i per tant es fonamenta en un fet poc intuïtiu. En aquest cas, el fet poc intuïtiu és que podem fer un model tan tan senzill del laberint que només necessitem pintar-lo de 2 colors!

El laberint màgic pintat de 2 colors.
A la imatge podeu veure el Laberint Màgic amb les habitacions pintades de dos colors. Les que tenen una carta senar son més clares i les que tenen una carta parell son més fosques. Aquest senzill model és tot el que es necessita per fer el truc de màgia!
Quan el mag elimina una habitació i aquesta habitació no és la nostra el primer que ens diu la intuïció és que el mag sap on som i només elimina caselles desocupades. Però el mag no necessita tanta informació. En té prou a fer servir un model matemàtic molt més senzill que li digui, només, si som a una casella clara o fosca. Així, si som a una casella clara eliminarà només caselles fosques i si som en una casella fosca eliminarà només caselles clares. Tant se val a quina casella en concret siguem!
Però com pot saber l’ordinador a quina casella hi som, si no li diem? Molt senzill, fixeu-vos que cada carta fosca està connectada només a cartes clares i a l’inrevés, però mai no podreu trobar un passadís que connecti dues cartes fosques o dues cartes clares. Això significa que si ets a una casella clara i fas un nombre senar de passos acabaràs en una casella fosca i a l’inrevés. Per contra, si fas un nombre parell de passos romandràs al mateix color del que vas sortir. De nou, al mag no li cal saber cap on vas, només li cal saber d’on has sortir i quantes habitacions has visitat!
Ara bé, el nombre de passos que fas te’l diu ell mateix així que només li cal encertar a quina casella ets a l’inici de la partida. Algú podria pensar que l’ordinador és prou intel·ligent com per endevinar en quin any vas néixer però, de nou, la resposta és molt més senzilla. Ets capaç de trobar-la?
Digues-nos a partir de quin moment l’ordinador pot estar segur de si et trobes en una habitació parell (fosca) o senar (clara) i com ho ha fet.
MMACA, Museu de Matemàtiques de Catalunya















Mot clara l’explicació
Queda molt elegant
Felicitat per l’empenta
molt bo 😉