Un món nou davant dels vostres ulls!
Ara que ja heu après què és la modelització matemàtica i com la fan servir els científics és hora de que busqueu i creeu els vostres propis models del món que us envolta.
Durant les darreres 4 setmanes hem fet un llarg viatge que ens ha dut a parlar amb científics de diverses universitats catalanes. Pel camí hem après què és la modelització i com s’utilitza avui dia per dur a terme projectes teòrics i aplicats en totes les branques de la ciència. Avui, ha arribat l’hora d’acomiadar-nos però abans volem fer una darrera repassada a tot allò que hem après i animar-vos a seguir investigant pel vostre compte, descobrint nous models i noves maneres d’aprendre d’ells.
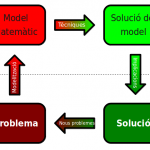
El cicle de la modelització
La modelització matemàtica és un procés iteratiu on la feina no acaba amb la solució d’un problema concret. De fet, cada solució incorpora nous enigmes, nous reptes a superar i cadascun d’aquests nous problemes ens fan créixer i avançar.
Malgrat que el concepte de modelització matemàtica es fa servir des de l’antiguitat, d’uns anys ençà els diferents passos que componen el cicle de la modelització han canviat ostensiblement.
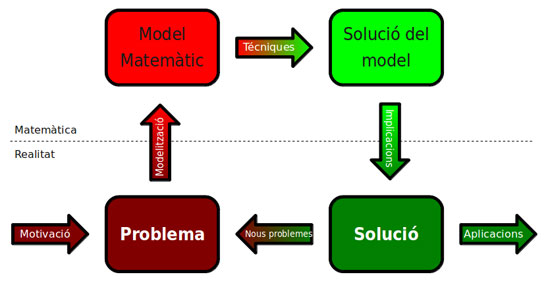
Cicle de la modelització.
Així, avui dia ens plantegem problemes que mai ens havíem plantejat, fem servir models que abans es consideraven irresolubles, trobem respostes amb noves eines i apliquem els nous coneixements a camps que fa uns anys ni tan sols existien.
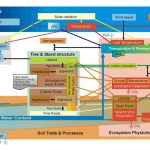
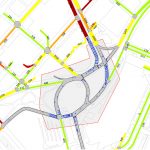
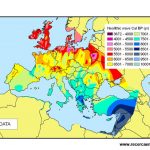
Aquestes setmanes hem vist exemples de tot tipus. L’Enrique ens plantejava un problema antic com és l’estudi de l’atmosfera on la física matemàtica fa anys que va proporcionar equacions precises però que no ha estat fins fa poc que hem pogut aplicar-les fent servir nous models i noves eines com ara l’ordinador. En Francesc fa servir l’àlgebra lineal, per resoldre problemes ben actuals com ara la planificació del transport públic d’una gran ciutat. En Carles utilitza una tècnica inspirada en la natura que fa uns anys ni tan sols coneixíem per estudiar els nostres boscos.
I no només els problemes, les tècniques i els camps d’aplicació han canviat. També les preguntes que fem als models són ben diferents. Així, abans, un model només era capaç de predir l’evolució d’un sistema (com fa la Cristina amb el soroll) o de determinar el valor de magnituds que no podíem mesurar directament (com fa en Joaquim amb l’arqueologia) però ara podem demanar-li que ens proporcionin la millor solució al nostre problema (com fan en Francesc i en Carles amb els seus problemes de transport i de conservació d’ecosistemes) o fins i tot observar-lo detingudament per entendre el comportament d’un fenomen complex (com fa l’Enrique amb les atmosferes).
Complexitat creixent
Amb l’arribada de noves eines matemàtiques i computacionals els científics han pogut afrontar models cada cop més complexos. De manera que, on abans només podíem estudiar casos senzills i homogenis ara podem treballar amb sistemes heterogenis que interaccionen de manera complexa.
Aquesta nova ciència de la complexitat, com alguns l’anomenen, és un corrent de pensament que actualment s’està imposant amb força l’àmbit científic, canviant la manera que tenim d’entendre i utilitzar els models.
On abans calia justificar cada variable que apareixia en un model ara només cal demostrar que el model es comporta de la mateixa manera que el fenomen que estem estudiant. On abans un model consistia en unes equacions i s’havia de resoldre de manera exacta “a mà” fent servir eines matemàtiques sofisticades ara ens permetem descriure els models algorítmicament i estudiar-los de manera probabilística gràcies a la força bruta computacional dels nostres ordinadors. On l’atzar no tenia cabuda ara pràcticament no és mai absent.
Així, a poc a poc, la nostra manera de fer servir els models (i les mateixes matemàtiques!) per entendre el món que ens envolta està canviant lenta però inexorablement i ens permet entendre fenòmens emergents allà on abans només veiem caos (com els que es produeixen en una xarxa social o en una colònia de formigues).
Com veieu la modelització és una eina en plena efervescència i ho seguirà sent en un futur proper. No la perdeu de vista!
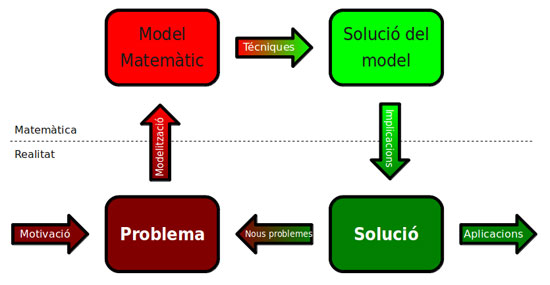
El cicle de la modelització
La modelització matemàtica és un procés iteratiu on la feina no acaba amb la solució d’un problema concret. De fet, cada solució incorpora nous enigmes, nous reptes a superar i cadascun d’aquests nous problemes ens fan créixer i avançar.
Malgrat que el concepte de modelització matemàtica es fa servir des de l’antiguitat, d’uns anys ençà els diferents passos que componen el cicle de la modelització han canviat ostensiblement.

Cicle de la modelització.
Així, avui dia ens plantegem problemes que mai ens havíem plantejat, fem servir models que abans es consideraven irresolubles, trobem respostes amb noves eines i apliquem els nous coneixements a camps que fa uns anys ni tan sols existien.
Aquestes setmanes hem vist exemples de tot tipus. L’Enrique ens plantejava un problema antic com és l’estudi de l’atmosfera on la física matemàtica fa anys que va proporcionar equacions precises però que no ha estat fins fa poc que hem pogut aplicar-les fent servir nous models i noves eines com ara l’ordinador. En Francesc fa servir l’àlgebra lineal, per resoldre problemes ben actuals com ara la planificació del transport públic d’una gran ciutat. En Carles utilitza una tècnica inspirada en la natura que fa uns anys ni tan sols coneixíem per estudiar els nostres boscos.
I no només els problemes, les tècniques i els camps d’aplicació han canviat. També les preguntes que fem als models són ben diferents. Així, abans, un model només era capaç de predir l’evolució d’un sistema (com fa la Cristina amb el soroll) o de determinar el valor de magnituds que no podíem mesurar directament (com fa en Joaquim amb l’arqueologia) però ara podem demanar-li que ens proporcionin la millor solució al nostre problema (com fan en Francesc i en Carles amb els seus problemes de transport i de conservació d’ecosistemes) o fins i tot observar-lo detingudament per entendre el comportament d’un fenomen complex (com fa l’Enrique amb les atmosferes).
Complexitat creixent
Amb l’arribada de noves eines matemàtiques i computacionals els científics han pogut afrontar models cada cop més complexos. De manera que, on abans només podíem estudiar casos senzills i homogenis ara podem treballar amb sistemes heterogenis que interaccionen de manera complexa.
Aquesta nova ciència de la complexitat, com alguns l’anomenen, és un corrent de pensament que actualment s’està imposant amb força l’àmbit científic, canviant la manera que tenim d’entendre i utilitzar els models.
On abans calia justificar cada variable que apareixia en un model ara només cal demostrar que el model es comporta de la mateixa manera que el fenomen que estem estudiant. On abans un model consistia en unes equacions i s’havia de resoldre de manera exacta “a mà” fent servir eines matemàtiques sofisticades ara ens permetem descriure els models algorítmicament i estudiar-los de manera probabilística gràcies a la força bruta computacional dels nostres ordinadors. On l’atzar no tenia cabuda ara pràcticament no és mai absent.
Així, a poc a poc, la nostra manera de fer servir els models (i les mateixes matemàtiques!) per entendre el món que ens envolta està canviant lenta però inexorablement i ens permet entendre fenòmens emergents allà on abans només veiem caos (com els que es produeixen en una xarxa social o en una colònia de formigues).
Com veieu la modelització és una eina en plena efervescència i ho seguirà sent en un futur proper. No la perdeu de vista!















Felicitats per les entrades les hem devorat rapidament
A veure si continueu amb d’altres projectes de matemàtiques
Prego feu la màxima difussió de les terceres jornades de modelització matemàtica que enguany es faran a Gandía el proper mes de juny.
Adjunto enllaç:
http://jornadasmoma3.blogs.upv.es/