Diari de recerca

Fa uns dies parlàvem amb Enrique García, de l’Observatori Esteve Duran, sobre els seus estudis de l’atmosfera de Júpiter i Saturn. Llavors vam aprendre que l’astronomia era una ciència que s’ha vist obligada històricament a substituir l’experimentació “de laboratori” per l’observació de fenòmens cada cop més llunyans. Així, allò que no es pot reproduir “a casa” s’ha buscat unes quantes galàxies més enllà amb aparells i tècniques cada cop més sofisticades.
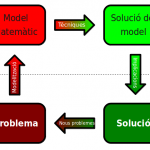
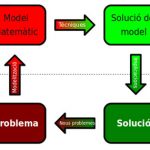
Des de fa uns quants anys, però, l’astronomia disposa d’una nova eina per estudiar l’univers, una eina que li permet, per primera vegada, experimentar. Aquesta nova eina és la simulació. I, com ja us deveu imaginar, tota simulació té al darrere un model matemàtic. Avui veurem quines peculiaritats tenen els models matemàtics que permeten simular planetes sencers!
Mecànica de Fluids
Els planetes “gasosos”, com ara Júpiter i Saturn, són un bon tema d’estudi. Ens poden ajudar a entendre un munt de coses sobre una branca de la física anomenada Mecànica de Fluids. Així, si aprenem a simular l’atmosfera d’un planeta com ara Júpiter, potser podrem aplicar els nous coneixements a la nostra pròpia atmosfera o, fins i tot, generalitzar-los i establir noves lleis universals de la Mecànica de Fluids.
La qüestió ve de lluny, el mateix Arquimedes hi va treballar establint els primers resultats de la hidrostàtica. I al segle XIX van quedar establertes les equacions de Navier-Stokes, que modelitzen perfectament el comportament dels fluids newtonians. Malauradament aquestes equacions no les sabem resoldre analíticament (és a dir “a mà”) per a problemes prou complexos i cal recórrer a simplificacions o a simulacions per aplicar-les a problemes de la vida real.
Així doncs, tot i disposar de models “perfectes” cal fer servir altres i aquí és on entra en joc la feina de l’Enrique i el seu estudi d’atmosferes extraterrestres.
Un núvol de paràmetres
Una de les simplificacions que fa servir l’Enrique és suposar que l’atmosfera està dividida en petites masses d’aire que no intercanvien energia tèrmica entre elles. Això permet resoldre de manera eficient les equacions dins de cada petit “compartiment” i, a més a més, simplifica els càlculs relacionats amb la interacció entre ells.
D’altra banda, a planetes gegants gasosos com Júpiter o Saturn no cal preocupar-se per les distorsions que afegeix el fregament entre la superfície planetària i l’atmosfera i es pot considerar que tots els “compartiments” són homogenis.
Tot i aquestes simplificacions, el model encara necessita que fixem tres tipus de paràmetres. D’una banda cal escollir els paràmetres corresponents al planeta que volem simular com ara la seva mida o la composició de la seva atmosfera. D’altra banda cal escollir les condicions inicials, la temperatura, pressió i velocitat del vent a cada punt. Finalment cal escollir la resolució numèrica que tindrà el nostre model, és a dir, la mida dels “compartiments” que farem servir i la velocitat de la simulació.
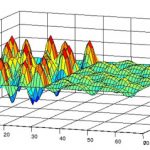
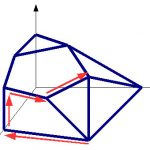
Aquests darrers paràmetres són comuns a tots els models que volen simular computacionalment un fenòmen continu ja que els ordinadors només poden treballar amb valors discrets, com ara els nombres naturals, o les xarxes de comunicació. Així, sempre que vulguem simular un fenòmen que té lloc en un mitjà continu, com ara l’atmosfera, cal discretitzar-ho primer: trencar el problema en “compartiments” de mida molt petita, tant pel que fa a l’espai com pel que fa al temps.

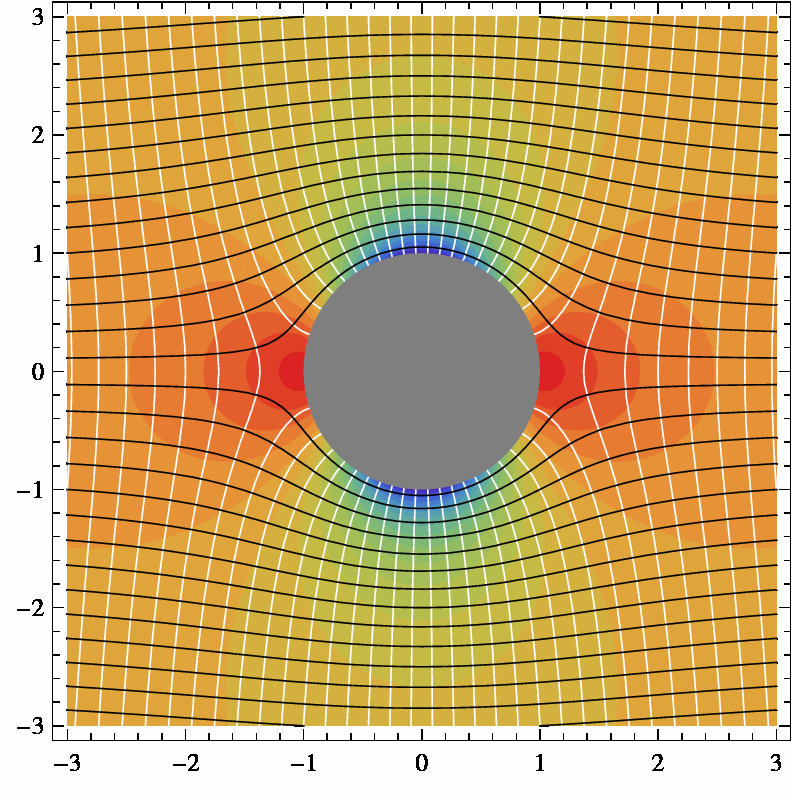
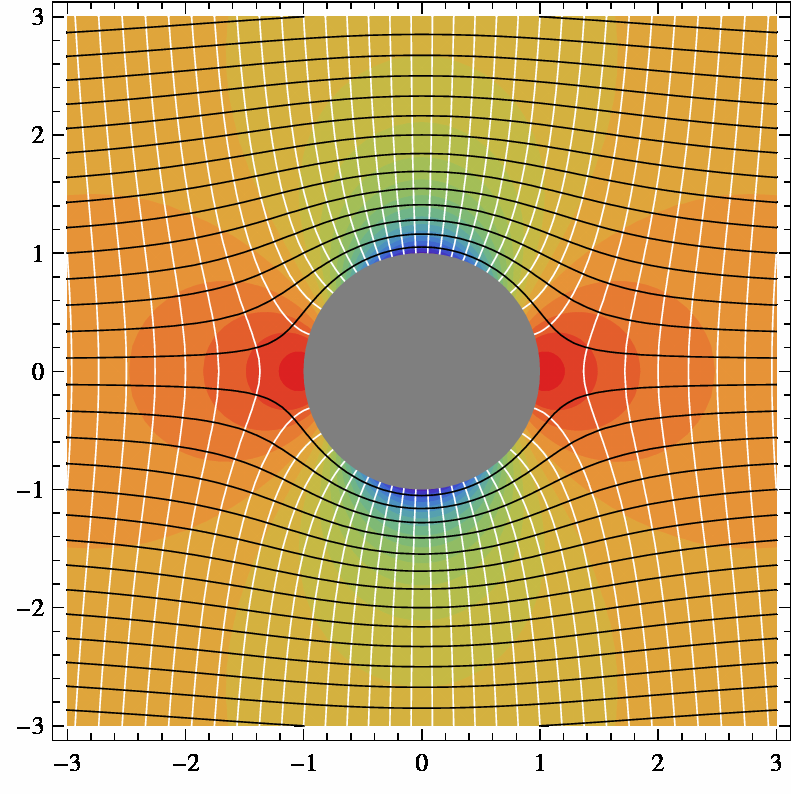
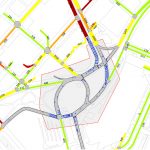
Simulació del pas d’un objecte circular a través d’un fluid.
Validant el model i treient-ne profit
Un cop s’ajusten els diferents paràmetres cal validar els resultats. A tal efecte es simulen situacions conegudes i es mesura l’error que comet el model. Només si el model aconsegueix simular amb èxit situacions que ens són ben conegudes podem plantejar-nos fer-lo servir per a simular fenòmens que no podem observar.
Finalment, un cop validat el model quedarà a càrrec del científic plantejar-li condicions inicials (experiments!) prou interessants com per extreure’n informació rellevant.