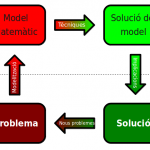
Hom podria pensar que el més natural és tenir un problema i després crear les eines per resoldre-ho. De vegades, però, els matemàtics creen models sense cap finalitat concreta i no és sinó molts anys després que algú troba un camp d’aplicació per a ells.
Un d’ells és el puzle dels Gratacels. Hi heu jugat ja?
El joc consisteix a col·locar una sèrie d’edificis en una quadrícula de 16 caselles de manera que compleixin la normativa vigent (que diu que a cada filera i a cada columna ha d’haver-hi exactament un edifici de cada tipus) i les exigències estètiques de l’arquitecte municipal (que imposen un determinat skyline des de cadascun dels 4 punts cardinals).
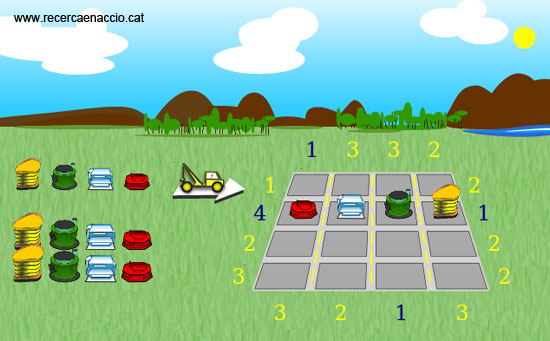
Aquest puzle, com passa gairebé sempre és més fàcil si es comença per les vores. En aquest cas, no ens referim literalment a les vores de la quadrícula sinó, més aviat, a les vores conceptuals del puzle: els casos extrems. Així, un cas extrem de skyline és aquell on només pots veure un edifici (que serà el més alt). Un altre cas, encara més extrem, serà aquell on pots veure tots 4 edificis (que, òbviament, estaran en ordre creixent).
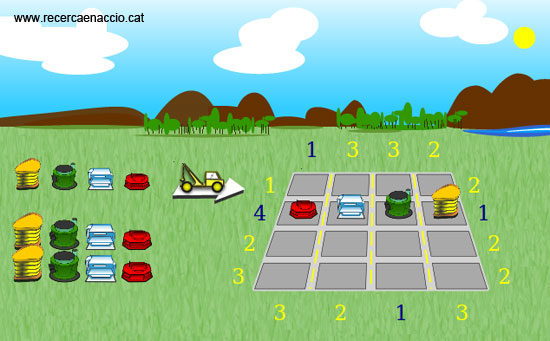
Exemple dels dos casos extrems mencionats.
Quadrats llatins
Leonhard Euler va ser un gran matemàtic del segle XVIII. Ronald Fisher va ser un dels millors estadístics del segle XX. Gairebé dos segles separen les vides d’aquests científics, però tot i així podem trobar un vincle entre ells: els quadrats llatins.
Tot va començar quan Leohard Euler va definir i estudiar les principals propietats dels quadrats llatins. Ho va fer des d’un punt de vista teòric, interessat potser a trobar quants n’hi havia o com es podien classificar, tot deixant que el seu instint matemàtic guiés la seva recerca sota criteris com ara l’elegància o la generalitat dels resultats que anava obtenint. La matemàtica disposava d’una nova eina per entendre el món, però encara ningú no havia trobat un problema on aplicar aquesta eina.
Uns 200 anys després Ronald Fisher va trobar una aplicació al model dels quadrats llatins descobert per Euler: reduir el nombre d’experiments necessaris per trobar quina era la millor fórmula química per a un nou fertilitzant. Amb el seu nou mètode, basat en els quadrats llatins de l’Euler, va poder aïllar els factors ambientals que podien afectar les proves, evitant així haver de repetir els experiments una i una altra vegada fins a estar segurs de quin era el millor producte.
És un exemple clàssic de com una eina matemàtica es pot crear molt abans que el problema que finalment solucionarà. La història de la ciència és plena de casos com aquest.
Ara et toca a tu!
Ja has conegut la història de Leonhard Euler i en Ronald Fisher. Ara tens l’oportunitat de posar-te a la pell d’aquests científics raonant una estona respecte a aquestes dues preguntes:
El joc consisteix a col·locar una sèrie d’edificis en una quadrícula de 16 caselles de manera que compleixin la normativa vigent (que diu que a cada filera i a cada columna ha d’haver-hi exactament un edifici de cada tipus) i les exigències estètiques de l’arquitecte municipal (que imposen un determinat skyline des de cadascun dels 4 punts cardinals).
Aquest puzle, com passa gairebé sempre és més fàcil si es comença per les vores. En aquest cas, no ens referim literalment a les vores de la quadrícula sinó, més aviat, a les vores conceptuals del puzle: els casos extrems. Així, un cas extrem de skyline és aquell on només pots veure un edifici (que serà el més alt). Un altre cas, encara més extrem, serà aquell on pots veure tots 4 edificis (que, òbviament, estaran en ordre creixent).

Exemple dels dos casos extrems mencionats.
Quadrats llatins
Leonhard Euler va ser un gran matemàtic del segle XVIII. Ronald Fisher va ser un dels millors estadístics del segle XX. Gairebé dos segles separen les vides d’aquests científics, però tot i així podem trobar un vincle entre ells: els quadrats llatins.
Tot va començar quan Leohard Euler va definir i estudiar les principals propietats dels quadrats llatins. Ho va fer des d’un punt de vista teòric, interessat potser a trobar quants n’hi havia o com es podien classificar, tot deixant que el seu instint matemàtic guiés la seva recerca sota criteris com ara l’elegància o la generalitat dels resultats que anava obtenint. La matemàtica disposava d’una nova eina per entendre el món, però encara ningú no havia trobat un problema on aplicar aquesta eina.
Uns 200 anys després Ronald Fisher va trobar una aplicació al model dels quadrats llatins descobert per Euler: reduir el nombre d’experiments necessaris per trobar quina era la millor fórmula química per a un nou fertilitzant. Amb el seu nou mètode, basat en els quadrats llatins de l’Euler, va poder aïllar els factors ambientals que podien afectar les proves, evitant així haver de repetir els experiments una i una altra vegada fins a estar segurs de quin era el millor producte.
És un exemple clàssic de com una eina matemàtica es pot crear molt abans que el problema que finalment solucionarà. La història de la ciència és plena de casos com aquest.
Ara et toca a tu!
Ja has conegut la història de Leonhard Euler i en Ronald Fisher. Ara tens l’oportunitat de posar-te a la pell d’aquests científics raonant una estona respecte a aquestes dues preguntes:
- Quants puzles dels gratacels de mida 4×4 pot haver-hi?
- Se t’acudeixen altres aplicacions dels quadrats llatins?











Son molt avurrits no fas re guay.