Gestionar el transport públic d’una gran ciutat és una tasca realment complicada en la qual s’han de resoldre múltiples problemes. Afortunadament, molts d’ells es poden escriure en el mateix “idioma”.
Fa uns dies ja vam parlar dels problemes relacionats amb la planificació del transport públic d’una gran ciutat. Escollir el traçat, la freqüència de pas i el tipus de vehicle que farà cada ruta tenint en compte les interaccions que es produeixen entre elles i amb la resta del trànsit és un problema que posa a prova a milers d’experts en investigació operativa.
Avui hem tornat a visitar la UPC perquè Francesc López ens acabi d’explicar com poden resoldre tots aquests problemes fent servir eines d’àlgebra lineal.
De l’àlgebra a la investigació operativa passant per la geometria
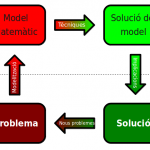
Per resoldre molts dels problemes que tracta en la seva investigació, en Francesc fa servir, entre d’altres, l’algorisme del Símplex. Aquest algorisme permet resoldre un tipus específic de models matemàtics així que el primer que cal fer és reescriure el problema en forma d’inequacions lineals.
Cada inequació lineal estarà associada a una restricció del nostre problema. Així, per exemple, hi haurà una que dirà que dues línies no poden passar pel mateix lloc a la vegada, hi haurà una altra que dirà que cada vehicle només podrà fer-se servir en una línia i que els usuaris que entren en un punt al metro n’han de sortir per un altre.
Com veieu, moltes d’aquestes restriccions són “de calaix” però cal recordar que per a l’ordinador només són inequacions i que som nosaltres, els qui les interpretem, els qui ens hem d’assegurar que tota solució “absurda” queda fora del nostre model. De fet, tot sovint expressar aquestes restriccions en forma d’inequació lineal no resulta gens senzill i bona part de la feina rau a trobar una bona combinació d’inequacions i demostrar que realment funciona.
Un cop reescrit el nostre model fent servir inequacions lineals l’algorisme del símplex l’interpreta com un poliedre en moltes dimensions. Així, cada inequació és un pla de tall que deixa fora algunes solucions “impossibles” i deixa dins tota la resta. Si anem afegint més inequacions el que passa és que cada cop queden menys solucions possibles dins del nostre model i com si fóssim escultors anem creant, cara a cara, el políedre de les solucions factibles.
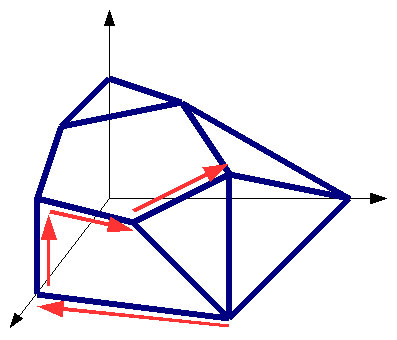
Políedre de dimensió 3.
Finalment a partir d’aquí l’algorisme del símplex cerca un vèrtex del nostre políedre i va resseguint les arestes fins a trobar la solució òptima.
Més dimensions = més problemes.
A la imatge podeu veure un exemple en 3 dimensions però els problemes amb els quals treballen els experts en planificació urbana poden arribar a tenir milions de variables i altres tantes dimensions. Com més dimensions i més cares té el poliedre associat al nostre problema més dificultats tindrà l’algorisme del símplex per a trobar la solució òptima.
Així, tot i que l’algorisme del símplex ens proporciona sempre una solució òptima i que els problemes escrits en forma de inequacions lineals tenen propietats matemàtiques que ens ajuden a resoldre’ls no sempre n’hi ha prou i de vegades cal fer servir tècniques encara més sofisticades.
Avui hem tornat a visitar la UPC perquè Francesc López ens acabi d’explicar com poden resoldre tots aquests problemes fent servir eines d’àlgebra lineal.
De l’àlgebra a la investigació operativa passant per la geometria
Per resoldre molts dels problemes que tracta en la seva investigació, en Francesc fa servir, entre d’altres, l’algorisme del Símplex. Aquest algorisme permet resoldre un tipus específic de models matemàtics així que el primer que cal fer és reescriure el problema en forma d’inequacions lineals.
Cada inequació lineal estarà associada a una restricció del nostre problema. Així, per exemple, hi haurà una que dirà que dues línies no poden passar pel mateix lloc a la vegada, hi haurà una altra que dirà que cada vehicle només podrà fer-se servir en una línia i que els usuaris que entren en un punt al metro n’han de sortir per un altre.
Com veieu, moltes d’aquestes restriccions són “de calaix” però cal recordar que per a l’ordinador només són inequacions i que som nosaltres, els qui les interpretem, els qui ens hem d’assegurar que tota solució “absurda” queda fora del nostre model. De fet, tot sovint expressar aquestes restriccions en forma d’inequació lineal no resulta gens senzill i bona part de la feina rau a trobar una bona combinació d’inequacions i demostrar que realment funciona.
Un cop reescrit el nostre model fent servir inequacions lineals l’algorisme del símplex l’interpreta com un poliedre en moltes dimensions. Així, cada inequació és un pla de tall que deixa fora algunes solucions “impossibles” i deixa dins tota la resta. Si anem afegint més inequacions el que passa és que cada cop queden menys solucions possibles dins del nostre model i com si fóssim escultors anem creant, cara a cara, el políedre de les solucions factibles.

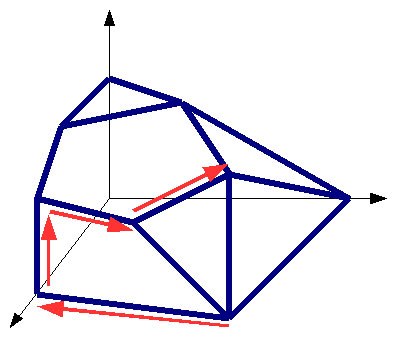
Políedre de dimensió 3.
Finalment a partir d’aquí l’algorisme del símplex cerca un vèrtex del nostre políedre i va resseguint les arestes fins a trobar la solució òptima.
Més dimensions = més problemes.
A la imatge podeu veure un exemple en 3 dimensions però els problemes amb els quals treballen els experts en planificació urbana poden arribar a tenir milions de variables i altres tantes dimensions. Com més dimensions i més cares té el poliedre associat al nostre problema més dificultats tindrà l’algorisme del símplex per a trobar la solució òptima.
Així, tot i que l’algorisme del símplex ens proporciona sempre una solució òptima i que els problemes escrits en forma de inequacions lineals tenen propietats matemàtiques que ens ajuden a resoldre’ls no sempre n’hi ha prou i de vegades cal fer servir tècniques encara més sofisticades.















0 Comentaris