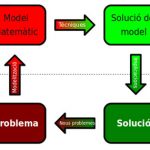
Quan el nostre model ens permet simular un fenomen podem fer-lo servir per prendre bones decisions. Malauradament, no sempre és fàcil.
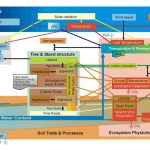
Carles Gracia ens va explicar fa uns dies que treballava en un model, anomenat GOTILWA+, que li permet simular l’evolució d’un bosc. Si introduïm els paràmetres propis del bosc i de la interacció amb la resta d’ecosistemes veïns (incloent-hi l’activitat humana!) podem predir amb força exactitud què li passarà al bosc en un futur: si creixerà, si apareixeran noves especies o si, senzillament, desapareixerà.
Aquesta eina ens permet predir, en certa manera, el futur però no ens diu com podem fer que el futur sigui millor. O si més no, no ens ho diu directament.
En el cas de la vibroacústica, que ens explicava la Cristina aquesta mateixa setmana, el procés era senzill, només calia saber si un determinat disseny complia la normativa o no, però en el cas d’en Carles el problema és més difícil: no ens conformem amb obtenir una solució vàlida sinó que a més, volem que sigui la millor!
Disposant d’un bon simulador, una persona amb prou paciència podria inspeccionar tots els futurs possibles i triar aquell que sigui òptim. Així, si poguéssim examinar totes les possibles combinacions de paràmetres el problema estaria resolt. Malauradament no és tan senzill, cada simulació pot resultar molt costosa (amb temps i recursos computacionals) i això significa que no podem examinar-les totes. Però llavors… com podem saber si ens hem deixat les millors solucions sense mirar?
Mil maneres d’estalviar-se feina
Els mètodes heurístics són aquells que serveixen per a trobar solucions de bona qualitat sense haver de mirar totes les solucions possibles. Sovint són el millor recurs que tenim per solucionar certs problemes.
Alguns mètodes heurístics es fonamenten en el sentit comú. Per exemple, els mètodes de Monte-Carlo examinen a l’atzar un gran nombre de solucions i es queden amb la millor. Òbviament ningú ens assegura que sigui la millor solució possible, però tenim motius estadístics per suposar que la millor solució trobada amb aquest mètode serà d’una qualitat raonablement bona.
Altres mètodes heurístics fan servir raonaments més elaborats i aprofiten qualsevol petit coneixement que l’investigador pugui aportar respecte al problema: quins paràmetres cal examinar més detingudament, quins són menys importants, quins grups de paràmetres es poden agrupar…
Finalment, hi ha tota una família de mètodes heurístics que s’inspira en la natura. Precisament un d’aquests mètodes és el que fa servir en Carles per obtenir respostes del seu model: optimització per eixams de partícules.

Un estol d’ocells es comporta de manera intel·ligent.
L’optimització per eixams de partícules s’inicia examinant un grapat de solucions possibles escollides a l’atzar.
A continuació la millor solució, entre les examinades, atreu a la resta de manera que cadascuna de les altres partícules del nostre eixam es mouen en direcció a la millor solució. És a dir, en la segona iteració tornarem a examinar un grapat de solucions però aquesta vegada, en comptes d’escollir-les a l’atzar les escollirem de manera que s’assemblin una mica més a la millor solució trobada fins el moment.
Aquest procés es repetirà diverses vegades (tantes com puguem!) i pot ser refinat afegint més d’un líder o ponderant els moviments segons la qualitat de cada partícula (així, les partícules que estiguin en una zona poc útil fugiran ràpidament cap a zones millors)
A més, per tal de no repetir simulacions, cada partícula es cuidarà de no apropar-se massa a cap altra de manera que mai no examinarem dues solucions que siguin similars i, per tant, cobrirem més terreny de l’espai de solucions.
Gràcies a aquesta tècnica es pot trobar ràpidament una combinació de paràmetres d’alta qualitat que, un cop examinada, ens dirà quins factors són els més determinants a l’hora de protegir els nostres boscos.
Aquesta eina ens permet predir, en certa manera, el futur però no ens diu com podem fer que el futur sigui millor. O si més no, no ens ho diu directament.
En el cas de la vibroacústica, que ens explicava la Cristina aquesta mateixa setmana, el procés era senzill, només calia saber si un determinat disseny complia la normativa o no, però en el cas d’en Carles el problema és més difícil: no ens conformem amb obtenir una solució vàlida sinó que a més, volem que sigui la millor!
Disposant d’un bon simulador, una persona amb prou paciència podria inspeccionar tots els futurs possibles i triar aquell que sigui òptim. Així, si poguéssim examinar totes les possibles combinacions de paràmetres el problema estaria resolt. Malauradament no és tan senzill, cada simulació pot resultar molt costosa (amb temps i recursos computacionals) i això significa que no podem examinar-les totes. Però llavors… com podem saber si ens hem deixat les millors solucions sense mirar?
Mil maneres d’estalviar-se feina
Els mètodes heurístics són aquells que serveixen per a trobar solucions de bona qualitat sense haver de mirar totes les solucions possibles. Sovint són el millor recurs que tenim per solucionar certs problemes.
Alguns mètodes heurístics es fonamenten en el sentit comú. Per exemple, els mètodes de Monte-Carlo examinen a l’atzar un gran nombre de solucions i es queden amb la millor. Òbviament ningú ens assegura que sigui la millor solució possible, però tenim motius estadístics per suposar que la millor solució trobada amb aquest mètode serà d’una qualitat raonablement bona.
Altres mètodes heurístics fan servir raonaments més elaborats i aprofiten qualsevol petit coneixement que l’investigador pugui aportar respecte al problema: quins paràmetres cal examinar més detingudament, quins són menys importants, quins grups de paràmetres es poden agrupar…
Finalment, hi ha tota una família de mètodes heurístics que s’inspira en la natura. Precisament un d’aquests mètodes és el que fa servir en Carles per obtenir respostes del seu model: optimització per eixams de partícules.

Un estol d’ocells es comporta de manera intel·ligent.
L’optimització per eixams de partícules s’inicia examinant un grapat de solucions possibles escollides a l’atzar.
A continuació la millor solució, entre les examinades, atreu a la resta de manera que cadascuna de les altres partícules del nostre eixam es mouen en direcció a la millor solució. És a dir, en la segona iteració tornarem a examinar un grapat de solucions però aquesta vegada, en comptes d’escollir-les a l’atzar les escollirem de manera que s’assemblin una mica més a la millor solució trobada fins el moment.
Aquest procés es repetirà diverses vegades (tantes com puguem!) i pot ser refinat afegint més d’un líder o ponderant els moviments segons la qualitat de cada partícula (així, les partícules que estiguin en una zona poc útil fugiran ràpidament cap a zones millors)
A més, per tal de no repetir simulacions, cada partícula es cuidarà de no apropar-se massa a cap altra de manera que mai no examinarem dues solucions que siguin similars i, per tant, cobrirem més terreny de l’espai de solucions.
Gràcies a aquesta tècnica es pot trobar ràpidament una combinació de paràmetres d’alta qualitat que, un cop examinada, ens dirà quins factors són els més determinants a l’hora de protegir els nostres boscos.















Quina passada, sembla talment una cacera de solucions